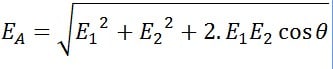√ Rumus Dan Cara Menghitung Medan Listrik Bersama Referensi Soal Dan Jawaban

Medan Listrik

Medan listrik ialah imbas yang ditimbulkan oleh keberadaan muatan listrik, menyerupai elektron, ion, atau proton, dalam ruangan yang ada di sekitarnya. Ia mempunyai satuan N/C atau dibaca Newton/Coulomb. Medan listrik umumnya dipelajari dalam bidang fisika dan bidang-bidang terkait dan secara tak pribadi juga di bidang elektronikayang telah memanfaatkan medan listrik ini dalam kawat konduktor (kabel).

 

Rumus matematika untuk medan listrik

Rumus ini sanggup diturunkan melalui Hukum Coulomb, yaitu gaya antara dua titik muatan:

Menurut persamaan ini, gaya pada salah satu titik muatan berbanding lurus dengan besar muatannya.

Medan listrik didefinisikan sebagai suatu konstan perbandingan antara muatan dan gaya:

Maka, medan listrik bergantung pada posisi. Suatu medan, merupakan sebuah vektor yang bergantung pada vektor lainnya. Medan listrik sanggup dianggap sebagai gradien dari potensial listrik. Jika beberapa muatan yang disebarkan menghasiklan potensial listrik, gradien potensial listrik dapat ditentukan.

 

Ilustrasi vektor listrik yang mengelilingi dua muatan titik yang berlawanan. Merah positif, hijau negatif. Sumber foto: Wikimedia Commons

 

Konstanta k

Dalam rumus listrik sering ditemui konstanta k sebagai ganti dari  (dalam goresan pena ini tetap dipakai yang terakhir), di mana konstanta  tersebut bernilai:

 N m² C^-2

yang kerap disebut konstanta kesetaraan gaya listrik. Konstanta gaya listrik atau konstanta kesetaraan gaya listrik atau k adalah suatu konstanta yang menyatakan kesetaraan antara gaya listrik, baik tarik-menarik atau tolak-menolak, antar dua buah muatan titik, yang dipisahkan dengan jarak tertentu, dengan hasil kali nilai kedua muatan dibagi kuadrat jarak pisahnya tersebut.

 

Cara menghitung medan listrik

Untuk menghitung medan listrik di suatu titik  akibat adanya sebuah titik muatan  yang terletak di  digunakan rumus

Penyederhanaan yang kurang tepat

Umumnya untuk melaksanakan penyederhanaan dipilih sentra koordinat berhimpit dengan titik muatan  yang terletak di  sehingga diperoleh rumus menyerupai telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:

dengan vektor satuan 

Disarankan untuk memakai rumusan yang melibatkan  dan  karena lebih umum, dan sanggup diterapkan untuk masalah lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu.

Penyederhanaan ini juga kadang menciptakan pemahaman dalam menghitungnya menjadi agak sedikit kabur. Selain itu pula lantaran penyederhanaan ini hanya merupakan salah satu masalah khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di sentra koordinat).

Tanda muatan listrik

Muatan listrik sanggup bernilai negatif, nol (tidak terdapat muatan atau jumlah satuan muatan positif dan negatif sama) dan negatif. Nilai muatan ini akan memengaruhi perhitungannya dalam hal tandanya, yaitu positif atau negatif (atau nol). Apabila pada setiap titik di sekitar sebuah (atau beberapa) muatan dihitung medan listriknya dan digambarkan vektor-vektornya, akan terlihat garis-garis yang saling berhubungan, yang disebut sebagai garis-garisnya. Tanda muatan memilih apakah garis-garis medan listrik yang disebabkannya berasal darinya atau menuju darinya. Telah ditentukan (berdasarkan gaya yang dialami oleh muatan uji positif), bahwa

• muatan positif (+) akan mengakibatkan garis-garis medan listrik berarah dari padanya menuju keluar.


• muatan negatif (-) akan mengakibatkan garis-garis medan listrik berarah menuju masuk padanya.


• muatan nol ( ) tidak mengakibatkan adanya garis-garis medan listrik.

Gradien potensial listrik

Medan listrik sanggup pula dihitung apabila suatu potensial listrik  diketahui, melalui perhitungan gradiennya:

dengan

untuk sistem koordinat Kartesius.

 

Energi medan listrik

Medan listrik menyimpan energi. Rapat energi suatu medan listrik diberikan oleh

dengan

 adalah permittivitas medium di mana medan listrik terdapat, dalam vakum .

 adalah vektor medan listrik.

Total energi yang tersimpan pada medan listrik dalam suatu volum  adalah

dengan

 adalah elemen diferensial volum.

 

Distribusi muatan listrik

Medan listrik tidak perlu hanya ditimbulkan oleh satu muatan listrik, melainkan sanggup pula ditimbulkan oleh lebih dari satu muatan listrik, bahkan oleh distribusi muatan listrik baik yang diskrit maupun kontinu. Contoh-contoh distribusi muatan listrik misalnya:

• kumpulan titik-titik muatan


• kawat panjang lurus berhingga dan tak-berhingga


• lingkaran kawat


• pelat lebar berhingga atau tak-berhingga


• cakram tipis dan cincin


• bentuk-bentuk lain

Kumpulan titik-titik muatan

Untuk titik-titik muatan yang tersebar dan berjumlah tidak terlalu banyak, medan listrik pada suatu titik (dan bukan pada salah satu titik muatan) sanggup dihitung dengan menjumlahkan vektor medan listrik di titik tersebut tanggapan oleh masing-masing muatan. Dalam masalah ini lebih baik dituliskan

yang dibaca, medan listrik di titik  akibat adanya muatan  yang terletak di . Dengan demikian medan listrik di titik {\displaystyle {\vec {r}}} akibat seluruh muatan yang tersebar dituliskan sebagai

di mana  adalah jumlah titik muatan. Sebagai ilustrasi, contohnya ingin ditentukan besarnya medan listrik pada titik  yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi , di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk masalah ini misalkan bahwa  dan  dan ambil sentra koordinat di titik  untuk memudahkan. Untuk masalah dua dimensi menyerupai ini, sanggup dituliskan pula

yang akan memberikan

sehingga

yang menghasilkan bahwa medan listrik pada titik tersebut ialah nol.

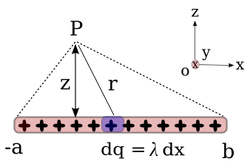
Kawat panjang lurus

Kawat panjang lurus merupakan salah satu bentuk distribusi muatan yang menarik lantaran bila panjangnya diambil tak-hingga, perhitungan muatan di suatu jarak dari kawat dan terletak di tengah-tengah panjangnya, menjadi amat mudah.

Untuk suatu kawat yang merentang lurus pada sumbu , pada jarak  di atasnya, dengan kawat merentang dari  sampai {\displaystyle b\!} dari titik proyeksi  pada kawat, medan listrik di titik tersebut sanggup dihitung besarnya, yaitu:

Seperti telah disebutkan di atas, apabila  dan  maka dengan memakai dalil L’Hospital diperoleh

Atau bila kawat diletakkan sejajar dengan sumbu-z dan bidang x-y ditembus kawat secara tegak lurus, maka medan listrik di suatu titik berjarak  dari kawat, sanggup dituliskan medan listriknya adalah

dengan  adalah vektor satuan radial dalam koordinat silinder:

di mana  adalah sudut yang dibuat dengan sumbu-x positif.

 

Resultan Medan Litrik yang Segaris

Jika Titik B berada di antara muatan Q1 dan Q2 yang terletak segaris. Makara ada dua medan listik yang timbul masing-masing oleh Q1 dan Q2. E1 ialah besar lengan berkuasa medan listrik lantaran dampak muatan Q1 dirumuskan:

Sedangkan E2 ialah medan listrik lantaran dampak muatan Q2, dirumuskan:

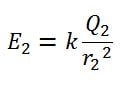
Besar besar lengan berkuasa medan listrik yang dialami oleh B ialah merupakan resultan vector dari E1 dan E2, dirumuskan:

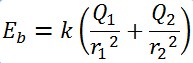
Hal yang perlu diperhatikan dalam memakai rumus diatas yaitu jenis muatan sumber dan muatan uji. Hal tersebut akan memilih + dan – dari medan listrik yang dialami.

 

Resultan Medan Listrik yang Tidak Segaris

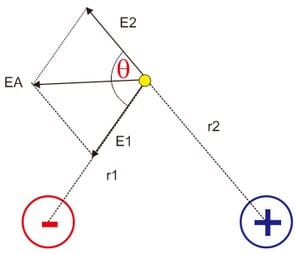
Dari gambar di atas, titik A berada dalam dampak medan listrik dari muatan Q1 dan Q2, sehingga antara titik Q1, A, dan Q2 membentuk sebuah sudut apit dengan nilai tertentu. Total besar lengan berkuasa medan listrik yang dialami oleh titik A ialah resultan dari vector E1 dan E2. Untuk memilih besarnya dipakai rumus resultan vektor.

 

 

Contoh Soal dan Jawaban Medan Listrik

1. Sepotong penggalan beling bermassa 5 mg bermuatan 2 μC. Kuat medan listrik yang diperlukan untuk menahan semoga potongan keca tersebut sanggup terapung di udara adalah…

A. 10 V/m

B. 1,8 V/m

C. 25 V/m

D. 100 V/m

E. 19,5 V/m

Pembahasan :

Agar potongan beling terapung di udara, maka:

⇒ Gaya berat = gaya listrik

⇒ W = Fc

⇒ m.g = q.E

⇒ (5 x 10^-6)(10) = (2 x 10^-6) E

⇒ E = 50/2

⇒ E = 25 V/m

Jawaban : C

 

2. Sebuah muatan uji +25.10⁵ C diletakkan dalam sbuah medan listrik. Jika gaya yang bekerja pada muatan uji tersebut ialah 0,5 N. Berapa besar medan listrik pada muatan uji tersebut?

Pembahasan:

Diketahui:

F= 0,5 N

q = +25. 10⁵ C

Ditanya: E ….?

Jawaban:

E = F/q

E = 0,5/25. 10⁵ C

E = 5. 10⁴ / 25 = 2000 N/C

 

Sebuah partikel yang bermuatan negatif sebesar 5 Coulomb diletakkan diantara dua buah keping yang mempunyai muatan berlawanan.

Jika muatan tersebut mengalami gaya sebesar 0,4 N ke arah keping B, tentukan besar besar lengan berkuasa medan listrik dan jenis muatan pada keping A!

Pembahasan dan jawaban:

F = QE

E = F / Q = 0,4 / 5 = 0,08 N/C

Untuk muatan negatif arah E berlawanan dengan F sehingga E berarah ke kiri dan dengan demikian keping B positif, keping A negatif.

 

3. Dua buah muatan titik +10μC dan -10 μC berada

pada jarak 20 cm di udara. Besar gaya yang dialami oleh muatan +1μC yang

terletak di tengah-tengah jarak antar kedua muatan tersebut adalah…

A. Nol

B. 4,5 N

C. 9,0 N

D. 18 N

E. 45 N

Pembahasan :

Karena

muatan +1μC terletak di tengah-tengah dua muatan yang tidak sejenis,

maka gaya coulomb yang dialami muatan  +1μC oleh muatan +10μC searah

dengan gaya coulomb oleh muatan -10μC.

Dengan demikian,

gaya coulomb total yang dialami muatan +1μC ialah gaya coulomb dari

muatan +10μC ditambah gaya coulomb oleh muatan -10μC.

Sehingga berlaku :

⇒ F = F₁ + F₂

⇒ F = k	10-6.10-5	+ k	10-6.10-5
	(10-1)2		(10-1)2

⇒ F = k	10-11	+ k	10-11
	10-2		10-2

⇒ F = k.10^-9 + k.10^-9

⇒ F = 2k.10^-9

⇒ F = 2 (9 x 10⁹).10^-9

⇒ F = 18 N

Jawaban : D

 

4. Sebuah konduktor berbentuk bola berongga dengan jari-jari 6 cm. Bila muatan bola tersebut 7 μC maka besar potensial listrik pada titik Q ialah … (k = 9.10⁹ N.m².C⁻² dan 1 μC = 10⁻⁶ C).

Pembahasan dan jawaban:

Besar muatan bola berongga adalah 

Q = 7 μC

= 7.10⁻⁶ C

Jarak titik Q dari sentra bola adalah 

r = (6 + 3) cm

= 9 cm

= 9.10⁻² m

Potensial listrik di titik Q yang berjarak r dari sentra bola adalah

= 7.10⁵

Jadi, besar potensial listrik di titik Q ialah 7.10⁵ volt (B).

 

5. Sebuah muatan uji +25.10⁵ C diletakkan dalam sbuah medan listrik. Jika gaya yang bekerja pada muatan uji tersebut ialah 0,5 N. Berapa besar medan listrik pada muatan uji tersebut?

Pembahasan:

Diketahui:

F= 0,5 N

q = +25. 10⁵ C

Ditanya: E ….?

Jawab :

E = F/q

E = 0,5/25. 10⁵ C

E = 5. 10⁴ / 25 = 2000 N/C

 

6. Sebuah elektron dengan massa 9,11 × 10⁻³¹ kg dan muatan listrik − 1,6 × 10⁻¹⁹ C, lepas dari katode menuju ke anode yang jaraknya 2 cm. Jika kecepatan awal elektron 0 dan beda potensial antara anode dan katode 200 V, maka elektron akan hingga di anode dengan kecepatan…

Pembahasan dan jawaban:

Data dari soal:

m_e = 9,11 × 10⁻³¹ kg

Q_e = − 1,6 × 10⁻¹⁹ C

ν₁ = 0 m/s

ΔV = 200 volt

ν₂ = ……. !?

Dengan aturan kekekalan energi mekanik, energi mekanik elektron ketika di anode sama dengan energi mekanik ketika di katode:

 

7. Dua buah partikel bermuatan berjarak R satu sama lain dan terjadi gaya tarik-menarik sebesar F.

Jika jarak antara kedua muatan dijadikan 4 R, tentukan nilai perbandingan besar gaya tarik-menarik yang terjadi antara kedua partikel terhadap kondisi awalnya!

Pembahasan dan jawaban:

sehingga

 

8. Titik A terletak di tengah-tengah dua buah muatan yang sama besar tetapi berlainan jenis yang terpisah sejauh a. Besar besar lengan berkuasa medan listrik di titik A ketika itu 36 NC^-1. Jika titik A tersebut digeser ¼ a mendekati salah satu muatan, maka besar besar lengan berkuasa medan listrik titik A sesudah digeser adalah…

A. 100 NC^-1

B. 96 NC^-1

C. 80 NC^-1

D. 60 NC^-1

E. 16 NC^-1

Pembahasan

Diketahui :

Muatan 1 (q₁) = +Q

Muatan 2 (q₂) = -Q

Jarak antara muatan 1 dan titik A (r_1A) = ½ a

Jarak antara muatan 2 dan titik A (r_2A) = ½ a

Kuat medan listrik di titik A (E_A) = 36 NC^-1

 

9. Dua buah muatan masing-masing 8 μC dan 2 μC diletakkan pada sumbu x

pada jarak 6 m satu sama lain. Muatan pertama terletak pada pusat

koordinat. Agar sebuah muatan negatif tidak mengalami gaya sedikitpun,

maka muatan ini harus diletakkan pada posisi…

A. x = -4 m

B. x = -2 m

C. x = 2 m

D. x = 4 m

E. x = 8 m

Pembahasan :

Misalkan q_A = 8 μC dan q_B = 2 μC

Agar

resultan gaya coulomb yang dialami oleh muatan negatif sama dengan nol

(tidak mengalami gaya sama sekali), maka arah gaya coulomb dari muatan 8

μC harus berlawanan arah dengan gaya coulomb dari muatan 2 μC dengan

besar yang sama sehingga saling meniadakan.

Karena

kedua muatan 8 μC dan 2 μC positif, maka muatan negatif harus diletakkan

di antara kedua muatan tersebut sehingga gayanya saling berlawanan

seperti pada gambar berikut:

Sehingga berlaku :

⇒ F = F_A – F_B

⇒ 0 = F_A – F_B

⇒ F_A = F_B

⇒ k	q.qA	= k	q.qB
	RA2		RB2

⇒	RB2	=	2 μC
	RA2		8 μC

⇒	RB2	=	1
	RA2		4

⇒ R_B² = ¼

R_A²

⇒ R_B = ½

R_A

Karena kita misalkan R_B = 6 – x, dan R_A = x, maka:

⇒ R_B = ½

R_A

⇒ 6 – x = ½x

⇒ 6 = ½x + x

⇒ 6 = 3/2 x

⇒ x = 12/3

⇒ x = 4 m sebelah kanan muatan 8 μC.

Jawaban : D

 

10. Dua buah partikel A dan B masing-masing bermuatan listrik +20 μC dan +45 μC terpisah oleh jarak 15 cm. Jika C ialah titik yang terletak di antara A dan B, sedemikian sehingga medan di C sama dengan nol, maka letak titik C dari partikel A adalah…

A. 2 cm

B. 3 cm

C. 4 cm

D. 6 cm

E. 8 cm

Pembahasan :

Dik : q_A = +20 μC, q_B = +45 μC, dan R = 15 cm

Karena

kedua muatan A dan B bernilai positif, maka muatan C sanggup diletakkan

di antara kedua muatan tersebut sehingga arah medan listrik yang

dihasilkan oleh A dan B berlawanan arah.

Agar sama dengan nol, maka

⇒ E_A = E_B

⇒ k	qA	= k	qB
	RA2		RB2

⇒	20	=	45
	x2		(15 – x)2

⇒	20	=	45
	x2		225 – 30x + x2

⇒ 45x² = 20(225 – 30x + x²)

⇒ 45x² = 4500 – 600x + 20x²

⇒ 25x² = 4500 – 600x

⇒ 25x² + 600x – 4500 = 0

⇒ x² + 24x – 180 = 0

⇒ (x + 30)(x – 6) = 0

⇒ x = -30 atau x = 6

Jadi, letak titik C dari partikel A ialah 6 cm.

Jawaban : D

 

11. Terdapat tiga muatan q₁, q₂, dan q₃ yang berada pada satu garis dengan q₂ berada di antara q₁ dan q₃. Jaraka antara q₁ dan q₂ ialah a sedangkan jarak antara q₂ dan q₃ ialah 0,5a. Muatan q₁ dan q₂ masing-masing +10μC, +20μC. Agar gaya coulomb yang dialami q₂ sama dengan nol, maka besar muatan q₃ adalah…

A. 2,5 μC

B. -2,5 μC

C. 25 μC

D. -25 μC

E. 4 μC

Pembahasan :

Gaya coulomb yang dialami oleh q₂ sanggup bernilai nol kalau gaya coulomb yang berasal dari muatan q₁ sama dengan gaya coulomb yang diberikan oleh muatan q₃. Dengan kata lain gaya coulomb tanggapan q₁ dan q₃ saling meniadakan.

Karena

muatan pertama dan muatan kedua positif, maka semoga gaya coulombnya

saling meniadakan (berlawanan arah), muatan ketiga harus positif.

Dengan demikian berlaku :

⇒ F₂₁ = F₂₃

⇒ k	q2 . q1	= k	q2 . q3
	(R21)2		(R23)2

⇒	q1	=	q3
	(R21)2		(R23)2

⇒	10	=	q3
	a2		(0,5a)2

⇒	10	=	q3
	a2		0,25a2

⇒ q₃ = 2,5μC

Jawaban : A

 

12. Kuat medan listrik sejauh 4 cm dari suatu muatan titik q sama dengan

10 N/C. Kuat medan listrik sejauh 8 cm dari muatan titik 6q sama dengan…

A. 20 N/C

B. 15 N/C

C. 12 N/C

D. 10 N/C

E. 6 N/C

Pembahasan :

Perbandingan besar lengan berkuasa medan listrik

⇒	E1	=	q1 . r22
	E2		q2 . r12

⇒	10	=	q .82
	E2		6q .42

⇒	10	=	4
	E2		6

⇒ E₂ = 60/4

⇒ E₂ = 15 N/C

Jawaban : B

 

13. Kuat medan listrik di satu titik P yang ditimbulkan oleh sebuah muatan q di titik asal O…

(1) Arahnya menjauhi q bila q positif, menuju q bila q negatif

(2) Berbanding pribadi dengan q

(3) Berbanding terbalik dengan kuadrat jarak OP

(4) Arahnya sama dengan gaya Coulomb pada muatan q’ di P bila q positif dan berlawanan dengan gaya coulomb tersebut bila q negatif.





Pembahasan :

Jika muatan q positif, maka arah garis medan ke luar menjauhi muatan q (ke luar). Sebaliknya kalau q bernilai negatif, maka arah garis medan listrik menuju muatan q (ke dalam).

Kuat medan listrik di suatu titik P yang berjarak r dari muatan q berbanding lurus dengan muatan q dan berbanding terbalik dengan kuadrat jarak. Secara matematis ditulis sebagai berikut:

E = k	q
	r2

Dengan :

E = besar lengan berkuasa medan listrik

k = tetapan

q = muatan

r = jarak titik ke muatan

Arah besar lengan berkuasa medan listriknya selalu sama dengan arah gaya Coulomb terhadap muatan q’ sebagai muatan uji. Jadi, opsi yang benar ialah 1, 2, dan 3.

Jawaban : A

 

14. Potensial listrik sejauh 4 cm dari muatan titik q sama dengan 10 V. Potensial listrik sejauh R dari muatan titik 5q sama dengan 20V. Nilai R sama dengan…

A. 6 cm

B. 7 cm

C. 8 cm

D. 9 cm

E. 10 cm

Pembahasan :

Dik : r₁ = 4 cm, r₂ = R, q₁ = q, q₂ = 5q, V₁ = 10V, V₂ = 20 V

Perbandingan potensial listrik :

⇒	V1	=	k.q1/r1
	V2		k.q2/r2

⇒	10	=	q/4
	20		5q/R

⇒	1	=	R
	2		5.4

⇒ R = 10 cm.

Jawaban : E

 

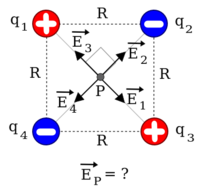
15. Empat buah muatan diletakkan di setiap sudut persegi yang panjang sisinya 10√2 cm. Jika O ialah titik perpotongan diagonal, maka besar lengan berkuasa medan listrik di titik O adalah…

A. 9 x 10⁶ N/C

B. 9√2 x 10⁶ N/C

C. 18 x 10⁶ N/C

D. 18√2 x 10⁶ N/C

E. 36√2 x 10⁶ N/C

Pembahasan :

Karena jarak dan besar muatan sama, maka medan listrik di titik O sanggup digambarkan menyerupai berikut:

Kuat medan listrik:

⇒ E = k	q
	r2

⇒ E = (9 x 109)	(10-5)
	(0,1)2

⇒ E = 9 x 10⁶ N

Kuat medan listrik di titik O:

⇒ E_o = √(2E)² + (2E)²

⇒ E_o = 2E √2

⇒ E_o = 2E √2

⇒ E_o = 2(9 x 10⁶) √2

⇒ E_o = 18√2 x 10⁶ N/C

Jawaban : D

 

Bacaan Lainnya

• Rumus Rangkaian Listrik Dan Contoh-Contoh Soal Beserta Jawabannya


• Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor


• Bagaimana Albert Einstein mendapat rumus E=mc² ?


• Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang


• Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender


• Cara Menghentikan Penindasan Bullying


• Cara menjaga keluarga Anda kondusif dari t3r0ris – Ahli anti-teror menerbitkan panduan praktis


• Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar


• Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan


• Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas


• Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita


• Apakah Produk Pembalut Wanita Aman?


• Sistem Reproduksi Manusia, Hewan dan Tumbuhan


• Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini


• Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?

 

Apakah Anda mempunyai sesuatu untuk dijual, disewakan, layanan apa saja yang ditawarkan atau lowongan pekerjaan?
Pasang iklan & promosikan jualan Anda kini juga! 100% GRATIS di: www.TokoPinter.com

 

3 Langkah super mudah: tulis iklan Anda, beri foto & terbitkan! semuanya di Toko Pinter

 

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar kalau Anda mengunduh aplikasi kita!

Siapa bilang mau pandai harus bayar? Aplikasi Ilmu pengetahuan dan gosip yang menciptakan Anda menjadi lebih smart!

• HP Android


• HP iOS (Apple)

 

Sumber bacaan: Physics Classroom, Tutor Vista

                       

 

Pinter Pandai “Bersama-Sama Berbagi Ilmu”

Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya

Sumber aciknadzirah.blogspot.com